Union Find Algorithm
An algorithm that implements find and union operations on a disjoint set data structure. It finds the root parent of an element and determines whether if two elements are in the same set or not. If two elements are at different sets, merge the smaller set to the larger set. At the end, we can get the connected components in a graph.
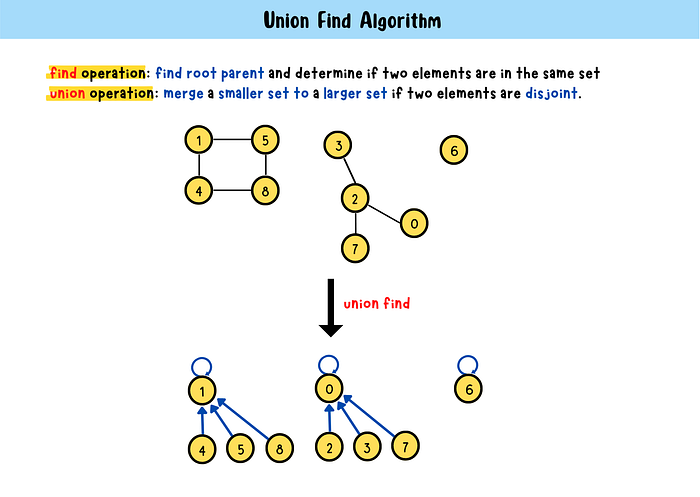
Table of Contents· Disjoint Set Data Structure
· Path Compression
· How Does Union Find Algorithm Work?
· Graphical Explanation
· Code Implementation
∘ Complexity
∘ Golang
∘ Python
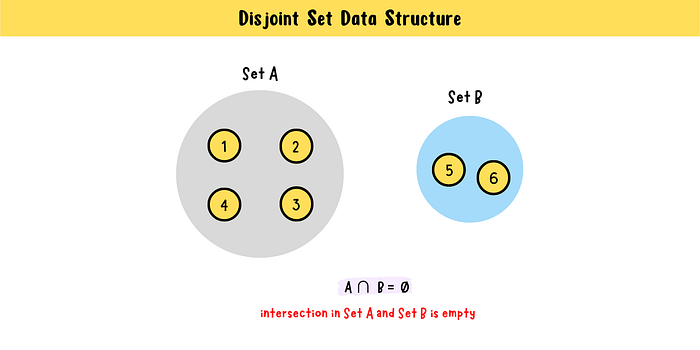
Disjoint Set Data Structure
Two or more sets have no element in common are called disjoint sets. Disjoint set data structure is also referred to as union find data structure because of its union and find operations.
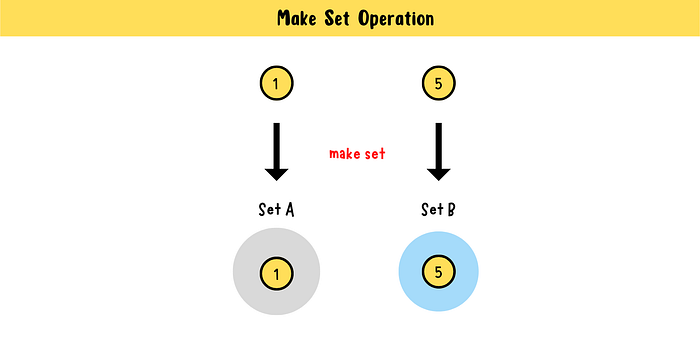
Disjoint set data structure supports three operations:
- Make Set: create a new disjoint set contains only the given element.
2. Find: determine which subset a given element belongs to. It is used to decide whether if two elements are disjoint or not.

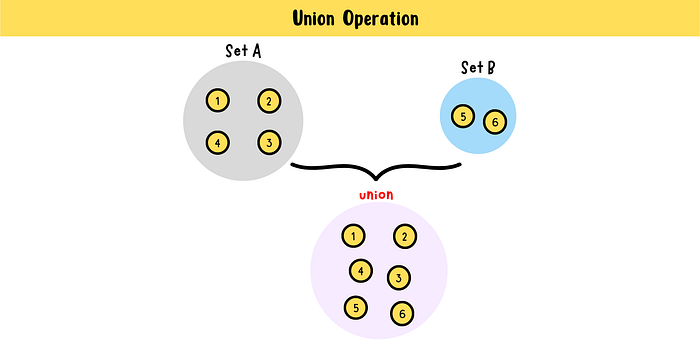
3. Union: merge two disjoint sets to a single disjoint set.
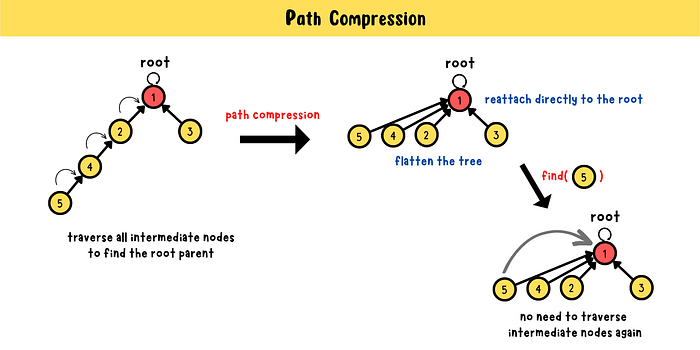
Path Compression
Path compression is a way to flatten the structure of the tree to make find operation more efficient. Find operation is used to find the root parent for a node. Without path compression, we have to travel upward the tree toward the root. The beauty of path compression is that we can find directly the root parent by reattaching visited nodes to the root.
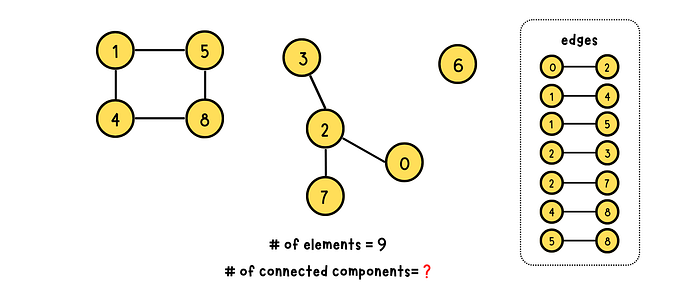
How Does Union Find Algorithm Work?
Union find algorithm performs the find operation to find a given element’s root parent and determine whether if two elements are in the same subset or not. If the two elements are in the same subset, they are already connected. Otherwise, they belong to different sets. Implement the union operation to merge the two disjoint sets to a signal set.
Graphical Explanation
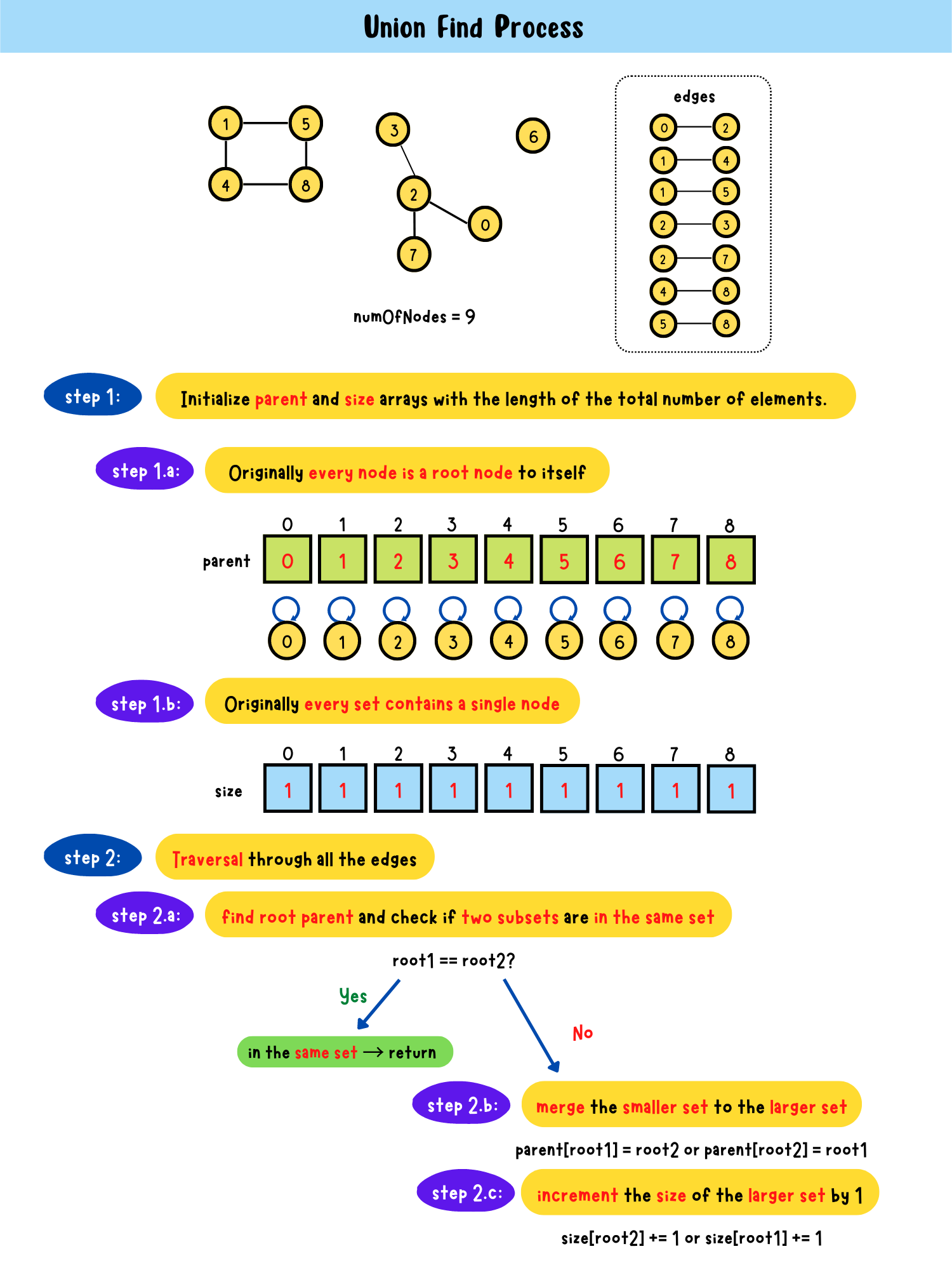
- step1: Initialize parent and size arrays with the length of the total number of elements.
parent: store a node's root parent
size: store the total number of elements in a subsetstep1.a: originally every node is a root node to itself
parent[i] = i
step1.b: originally every set contains a single node
size[i] = 1
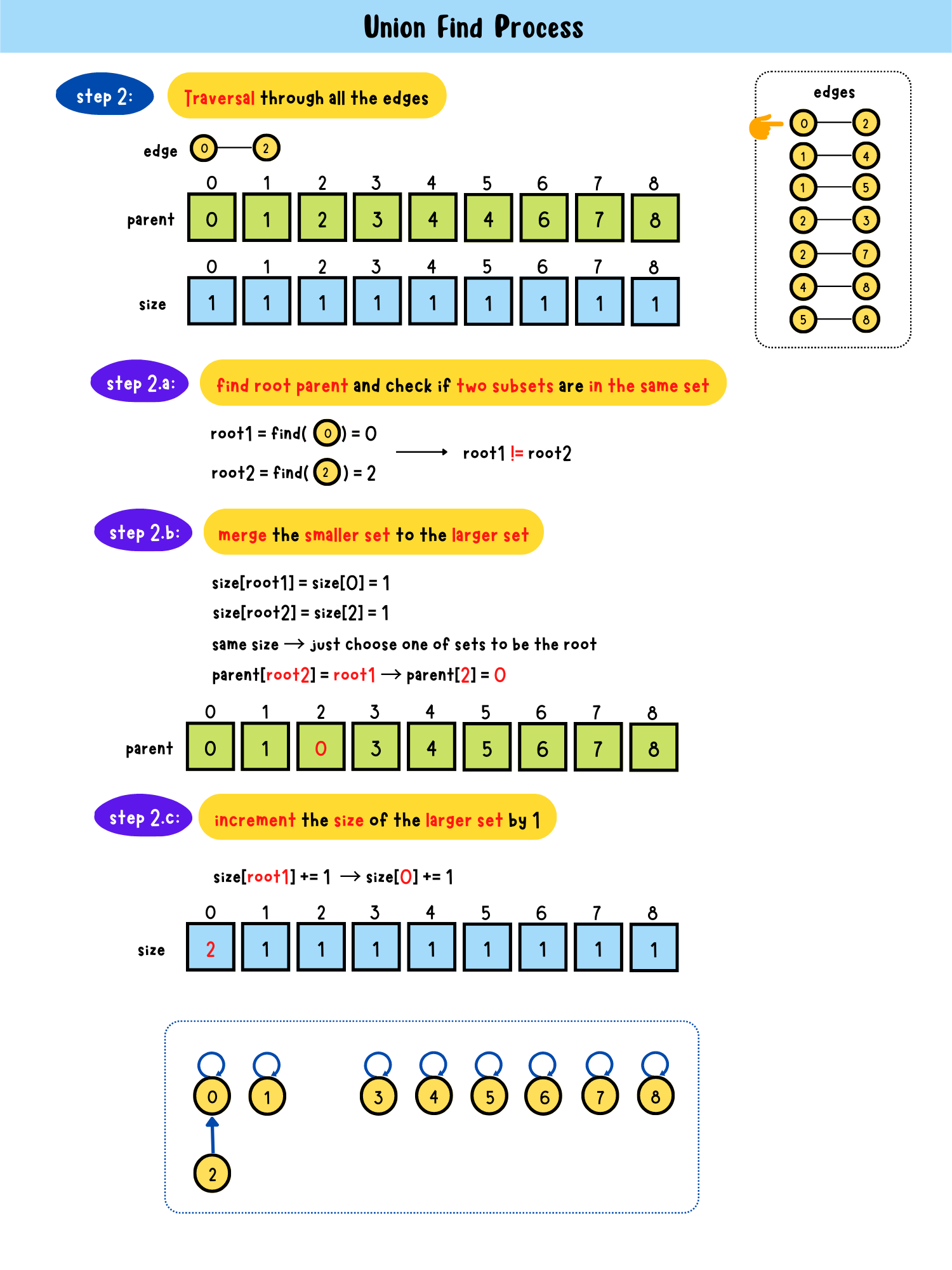
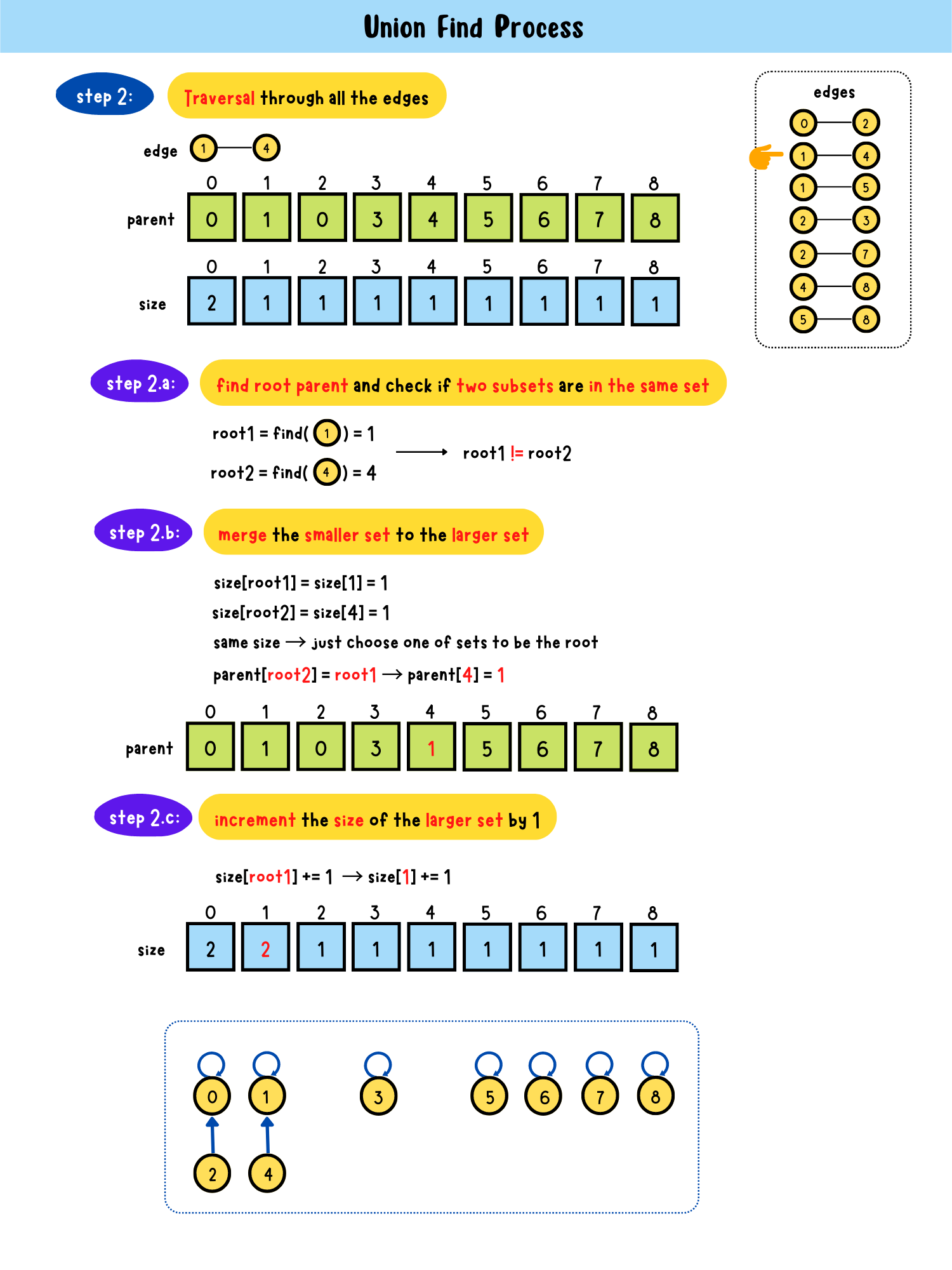
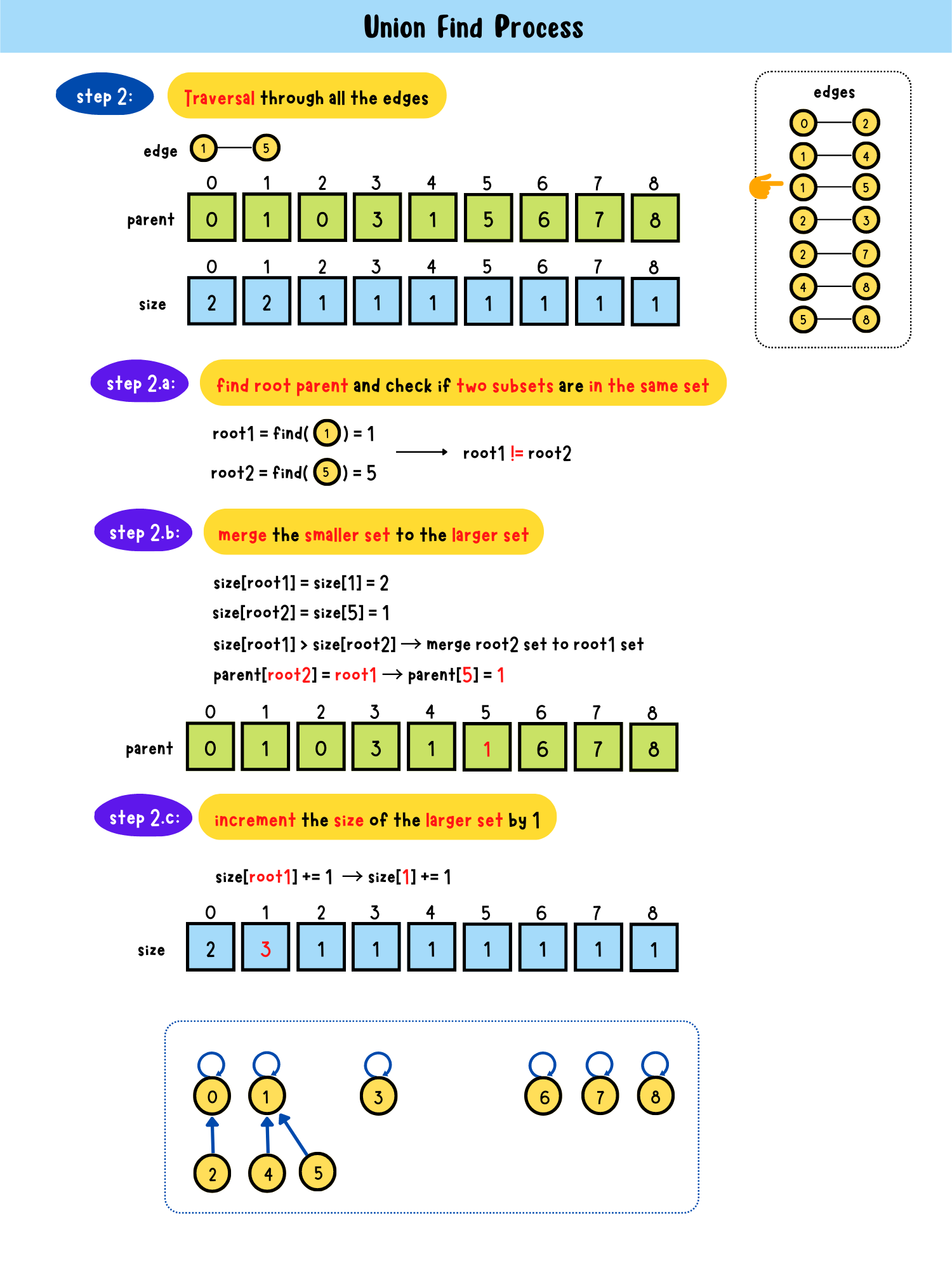
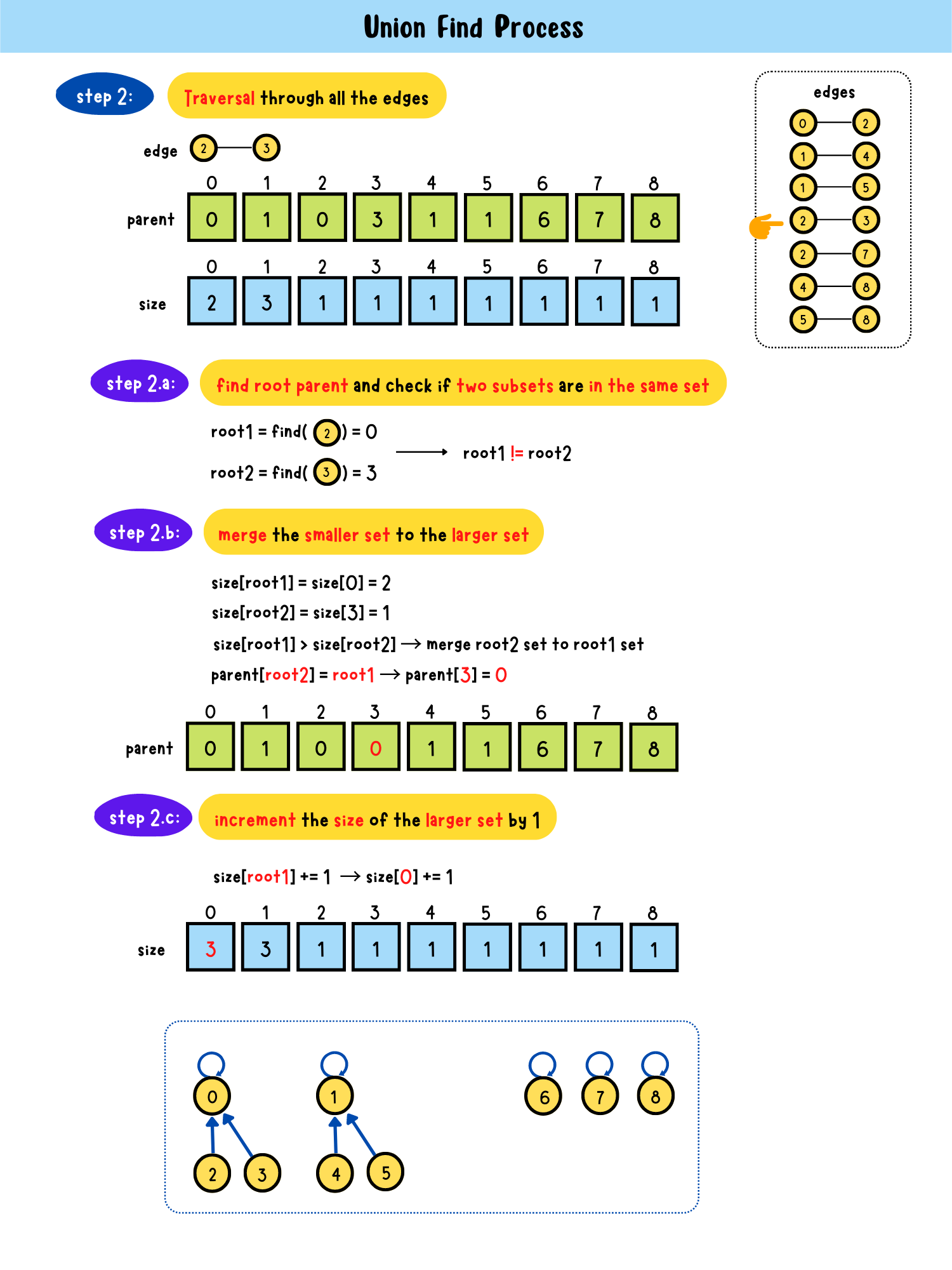
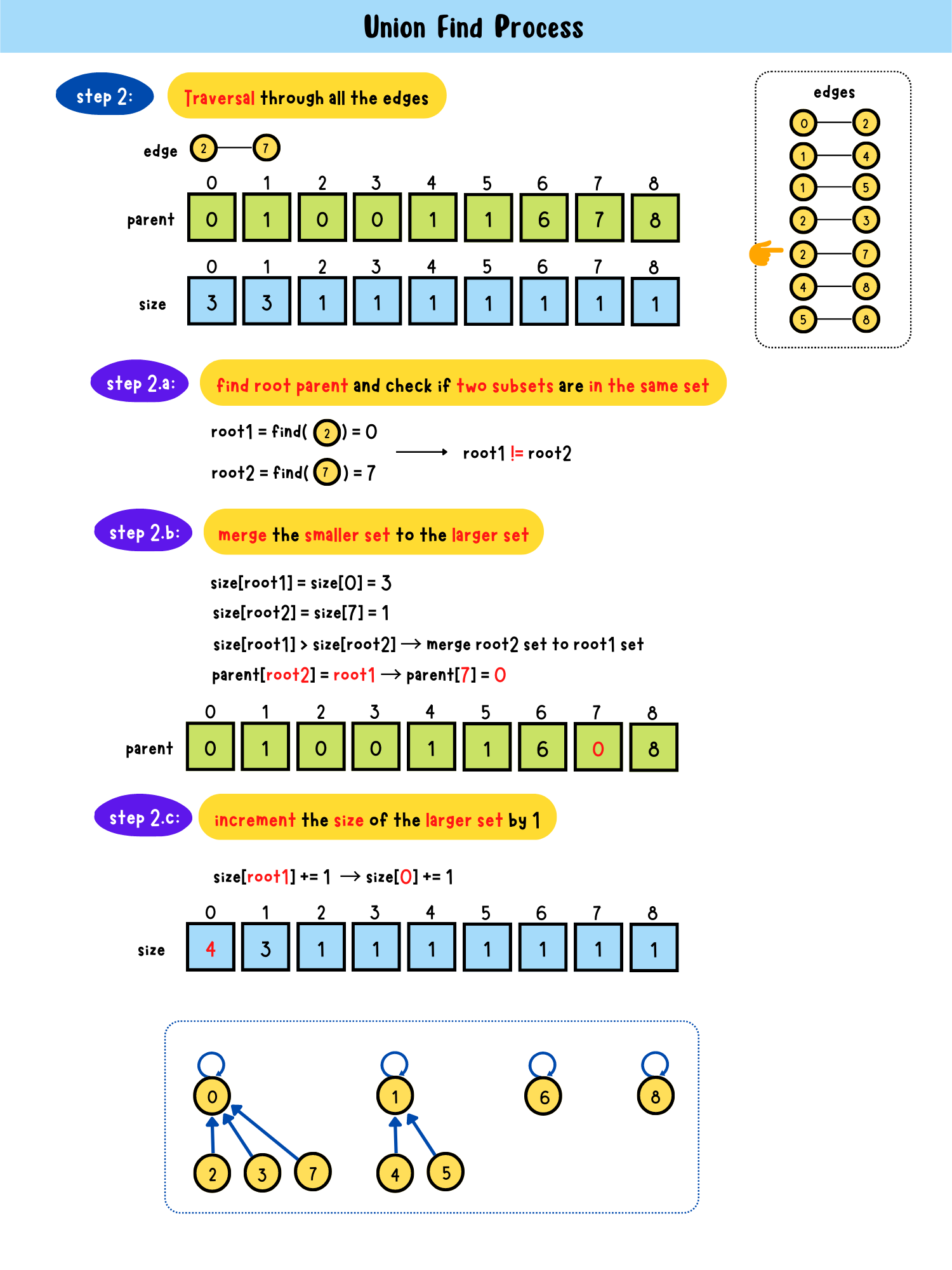
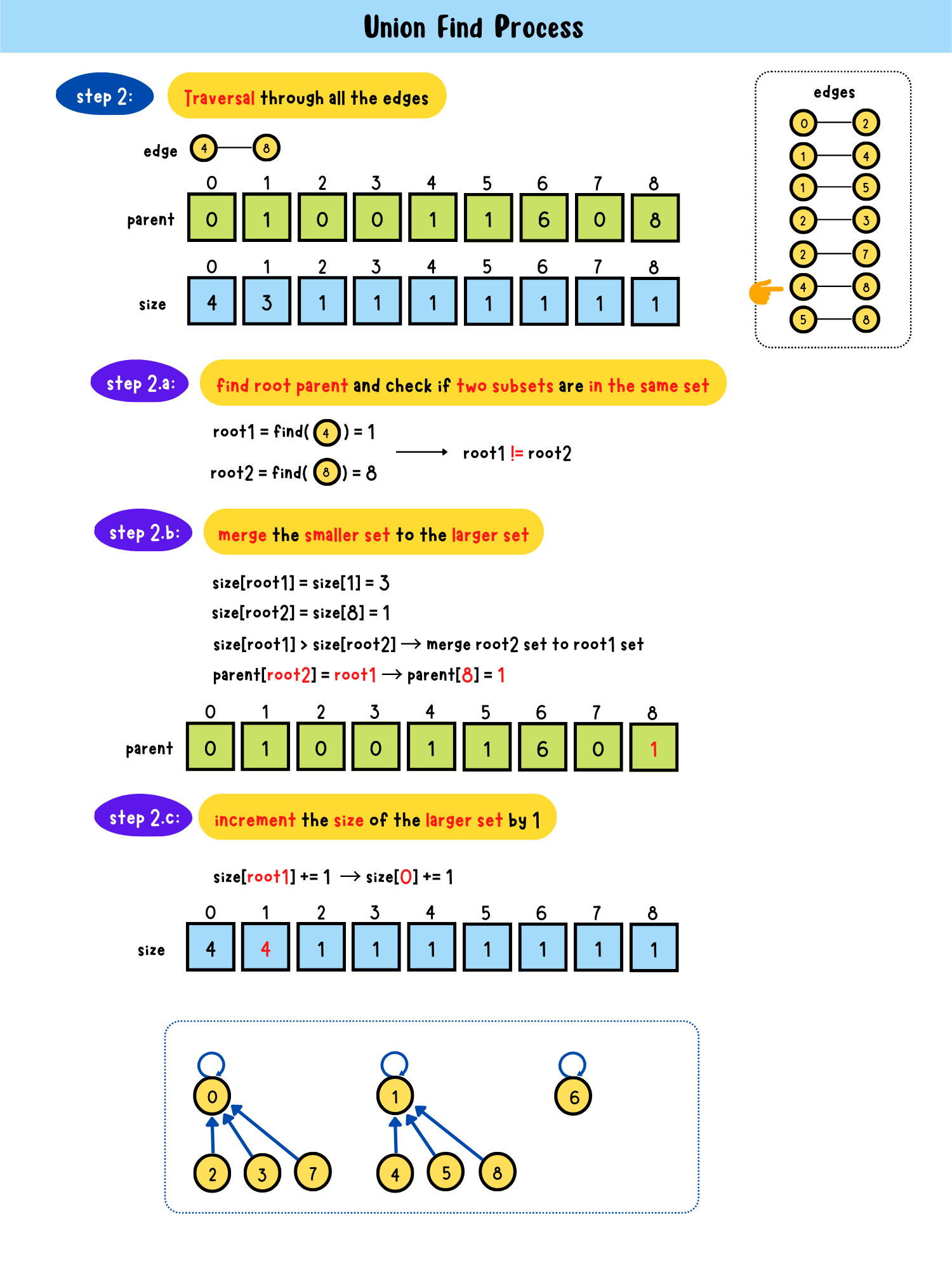
- step2: Traversal through all edges
step2.a: find root parent and check if two subsets are in the same setroot1 == root2?
- Yes → in the same set → return
- No → step2.bstep2.b: merge the smaller set to the larger set
parent[root1] = root2 or parent[root2] = root1step2.c: increment the size of the larger set by 1
size[root2] += 1 or size[root1] += 1

Code Implementation
Complexity
Time: O(nlog(n))
Space: O(n) parent and size array
n: the total number of nodes in the given graph
- Find operation
Time: O(log(n)) log(n) is the height of the tree
Space: O(1) - Union operation
Time: O(1)
Space: O(1)

